>재수 하는 학생인데요 (이학교 출신은 아니구요) >5등급 차이는 광도에서는 어떻게 차이가 나는가? 1등급과 3등급의 차이가 나는 경우 광도는 어떻게 다른가? >두 개의 알려진 별 A,B가 있다. 별 B는 별 A보다 10배 먼 거리에 있다. 두 별의 등급차는 얼마가 될까? >식변광성의 광도 곡선에서 다음의 문제에 답을 하라. >별 A가 별 B의 뒤에 있을때 약간의 밝기차가 생겼다고 하자. 별 B가 별A의 뒤에 있을때는 >그보다 훨씬 더 큰 밝기차가 관측되었다면 어떤 별의 광도가 더 큰가? 왜 그런가 이유를 설멸하시오. > >요 세문제가 안풀려서 선생님 답변좀 부탁 드립니다. > >
1. 광도와 등급 사이의 관계
등급은 광도를 로그 함수로 변환한 것입니다. 다시 말해,
![]()
입니다. 그런데, 등급은 상대적인 개념이므로 위와 같이 쓸 수는 없고, 두 등급의 비교만이 가능합니다. 다시 말해,
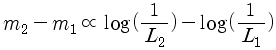
와
같이 쓸 수 있습니다. 로그 함수끼리의 뺄셈은 다음과 같이 바꿀 수 있죠.
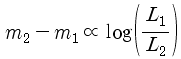
비례식을 등식으로 전환하려면 상수를 넣으면 되죠. 이 경우 상수는 2.5입니다.
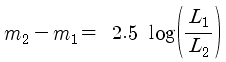
또는
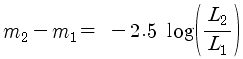
마지막
식에서 - 부호가 앞으로 나오는 대신 분자와 분모가 바뀌었죠.
그러면 이제 질문에 답해 볼까요..
1) 5등급 차이는 광도로 몇 배 차이인가?
별2의 등급이 별1의 등급보다 5등급 더 작다면 다음과 같이 쓸 수 있겠네요.
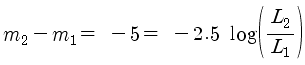
다음과
같이 바꾸어 쓸 수 있네요..
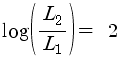
그러면
또 이렇게 되구요..
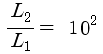
별2는
광도로 볼 때 별1의 100배가 되는군요.. 맞습니다. 5등급 더 작으면 광도는 100배가 됩니다.
2) 1등급 차이는 광도로 몇 배 차이인가?
그러면 1등급의 차이는..
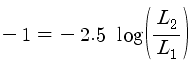
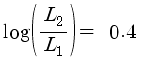
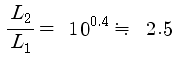
1등급
작으면 광도는 2.5배가 되지요..
3) 1등급과 3등급 차이는 광도로 몇 배 차이인가?
같은 방법으로 1등급과 3등급의 차이도 알 수 있습니다.
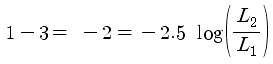
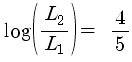
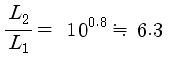
정리하여,
다음과 같이 이해할 수 있습니다.
1등급 작으면 --- 광도는 2.5배 더 크다.
2등급 작으면 --- 광도는 (2.5×2.5 ≒ 6)배 더 크다.
3등급 작으면 --- 광도는 (2.5×2.5×2.5 ≒ 16)배 더 크다.
4등급 작으면 --- 광도는 (2.5×2.5×2.5 ≒ 40)배 더 크다.
5등급 작으면 --- 광도는 (2.5×2.5×2.5 ≒ 100)배 더 크다.
6등급 작으면 --- 광도는 (2.5×2.5×2.5 ≒ 250)배 더 크다.
2.
거리와 등급 사이의 관계
광도는 별로부터 거리의 제곱에 반비례하여 감소합니다. 이것은 고등학교 1학년 과학의 파동에너지 부분에서 배운 내용입니다. 구면파의 에너지 세기는 거리에 반비례하여 감소한다고 배웠지요..
거리 r1과 r2에서의 광도를 각각 L1과 L2라고 하면
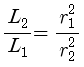
따라서,
거리가 10배 더 먼 별의 광도는 100배 더 작겠지요. 광도 100배 차이는 앞의 식을 통해 5등급 차이라는 것을 알 수 있습니다.
3. 식변광성의 밝기
별 A가 가려졌을 때보다 별 B가 가려졌을 때 밝기 차이가 더 크다면 대개의 경우 별 B의 광도가 더 큽니다.
별의 광도는 별의 반지름(R) 및 별의 표면온도(T)와 다음과 같은 관계를 가지고 있습니다.
![]()
σT4은 단위
면적이 내놓는 에너지의 양인데, 여기에 별의 표면적 4πR2을 곱한 것입니다.
이 식을 보면 별의 광도는 별의 반지름의 제곱에 비례하고, 표면온도의 네 제곱에 비례합니다.
이제 두 별의 광도를 합쳐서 생각해보도록 하죠. 두 별이 서로 가리지 않았을 때, 이 두 별의 광도의 합은 가장 클 것입니다.
만약, 한 별이 다른 별을 가린다면 광도는 그만큼 감소하겠죠. 두 별이 서로를 동일한 면적만큼 가린다고 하면, 저온의 별이 가려졌을 때보다 고온의 별이 가려졌을 때 광도의 합은 더 감소할 것입니다.
별 A가 가려졌을 때보다 별 B가 가려졌을 때 밝기가 더 많이 감소했다는 것으로 보아 별 B의 표면온도가 더 높다는 것을 알 수 있고, 두 별의 반지름이 비슷하다고 가정하면 별 B의 광도가 더 크다고 할 수 있습니다. 이것은 별 A가 별 B보다 더 크다고 하더라도 마찬가지입니다. 왜냐하면 광도는 표면온도에 대해서는 네제곱에 비례하고 반지름에 대해서는 제곱에 비례하기 때문입니다.